「Codeforces 916E」Jamie and Tree

发表于 | | 阅读次数:
字数统计: 1.6k 字

Description

题目链接：Codeforces 916E

给你一棵有根树标号为 $1\sim n$，每个点都有一个权值 $a_i$。初始时根为 $1$，接下来有 $q$ 次操作，操作分为以下 $3$ 种：

  • 1 x：将整棵树的根变为节点 $x$。
  • 2 x y k：把 $x,y$ 的 $\text{LCA}$ 为根的子树中的所有点的权值增加 $k$。
  • 3 x：查询以 $x$ 为根的子树中的节点的权值和。

数据范围：$1\le n,q\le 10^5$，$-10^8\le a_i,k\le 10^8$

Solution

如果没有换根操作，那么我们只需要对这棵树的 $\text{DFS}$ 序建立线段树，支持区间修改和区间查询。

接下来考虑换根操作。此时我们显然不能真的把根换掉，根只能一直为 $1$ 节点，而是要对根和操作的节点的关系进行分类讨论！

由于操作 $2$ 和操作 $3$ 在位置关系分析上的本质是相同的，所以我们只需要考虑位置关系和如何求 LCA 即可。

位置关系

设当前整棵树的根节点为 $R$，询问的子树根节点为 $X$，那么我们可以发现这两者存在以下 $3$ 种关系。

对于每种位置关系的图示，$R$ 和 $X$ 均标记在节点上，蓝色的节点表示需要被操作的节点。

  1. 如果 $R$ 就是 $X$：

    此时整棵树的所有节点都需要被操作。

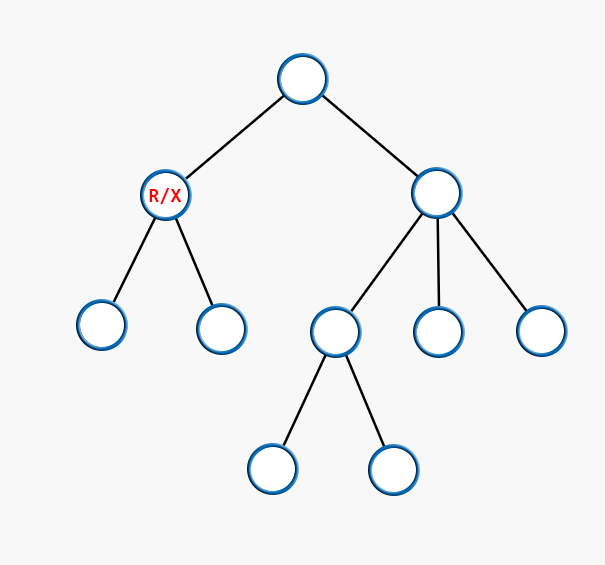
  2. 如果 $R$ 不在 $X$ 的子树内：

    此时我们可以发现 $X$ 这棵子树的形态与原图的形态一致，所以只要对以 $1$ 为根节点时的子树 $X$ 进行操作即可。

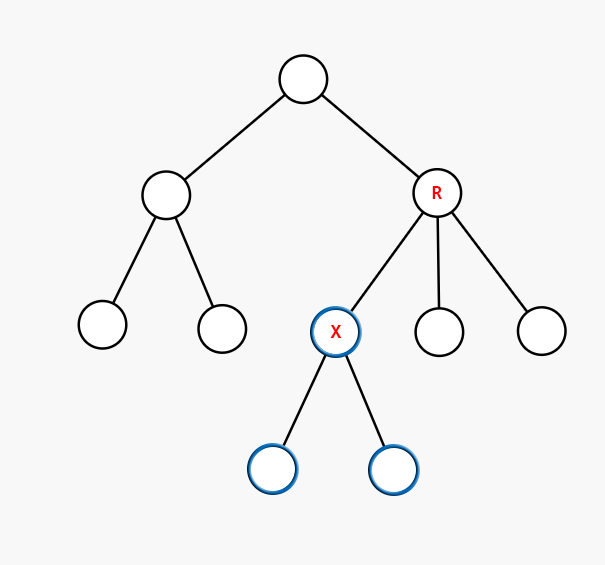
  3. 如果 $R$ 位于 $X$ 的子树内：

    此时情况比较复杂，需要被操作的节点为： 所有节点除去以 $X$ 到 $R$ 的路径上的第一个节点（这个点满足既是 $R$ 的祖先，又是 $X$ 的儿子）为根的子树。那么我们可以根据容斥原理，先对整棵树进行操作，再对那个子树进行相反的操作（如果是查询则减去贡献，如果是修改则减去）。

    那么怎么求这个点呢？我们记 $deep_i$ 表示 $i$ 在原图中的深度，让 $R$ 往上移动 $deep_R-deep_X-1$ 个点即可，这个过程显然可以用倍增实现。

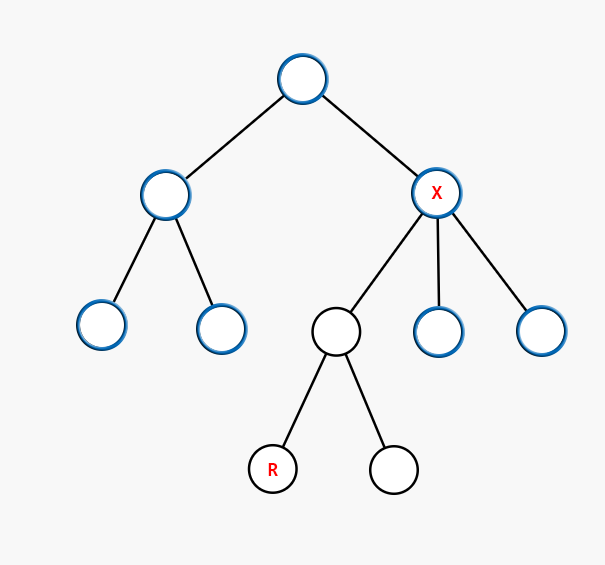
如何求 LCA

其实也是之前的分类讨论的套路啦！QAQ

设当前整棵树的根节点为 $r$，修改的节点为 $x,y$。在以 $1$ 为根节点的前提下，我们也可以分类讨论！（以下内容参考 $\text{Codeforces}$ 官方题解）

  1. 如果 $x,y$ 都在 $r$ 的子树内，那么 $\text{LCA}$ 显然为 $\text{LCA}(x,y)$。
  2. 如果 $x,y$ 只有一个在 $r$ 的子树内，那么 $\text{LCA}$ 肯定为 $r$。
  3. 如果 $x,y$ 都不在 $r$ 的子树内，我们可以先找到 $p=\text{LCA}(x,r)$，$q=\text{LCA}(y,r)$。如果 $p$ 和 $q$ 不相同，那么我们选择其中较深的一个；如果 $p$ 和 $q$ 相同，那么 $\text{LCA}$ 就是 $p$ 或 $q$。

综上所述，我们可以发现我们要求的 $\text{LCA}$ 就是 $\text{LCA}(x,y)$，$\text{LCA}(x,r)$，$\text{LCA}(y,r)$ 这三者中深度最大的！

时间复杂度：$O(n\log n)$（当然带着巨大常数）

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
 
#include <cstdio>
#include <algorithm>
#define lson rt<<1
#define rson rt<<1|1

const int N=1e5+5,M=2e5+5,logN=17+1;
int n,m,root,idx,a[N],f[N][logN],dfn[N],seq[N],sz[N],dep[N];
int tot,lnk[N],ter[M],nxt[M];
long long seg[N<<2],tag[N<<2];

void pushup(int rt) {
    seg[rt]=seg[lson]+seg[rson];
}
void build(int rt,int l,int r) {
    if(l==r) {
        seg[rt]=a[seq[l]];
        return;
    }
    int mid=(l+r)>>1;
    build(lson,l,mid);
    build(rson,mid+1,r);
    pushup(rt);
}
void update(int rt,int l,int r,long long k) {
    seg[rt]+=1LL*(r-l+1)*k;
    tag[rt]+=k;
}
void pushdown(int rt,int l,int r) {
    if(!tag[rt]) return;
    int mid=(l+r)>>1;
    update(lson,l,mid,tag[rt]);
    update(rson,mid+1,r,tag[rt]);
    tag[rt]=0;
}
void modify(int x,int y,int rt,int l,int r,int k) {
    if(x<=l&&r<=y) {
        update(rt,l,r,k);
        return;
    }
    pushdown(rt,l,r);
    int mid=(l+r)>>1;
    if(x<=mid) modify(x,y,lson,l,mid,k);
    if(mid<y) modify(x,y,rson,mid+1,r,k);
    pushup(rt);
}
long long query(int x,int y,int rt,int l,int r) {
    if(x<=l&&r<=y) return seg[rt];
    pushdown(rt,l,r);
    int mid=(l+r)>>1;
    long long ret=0;
    if(x<=mid) ret+=query(x,y,lson,l,mid);
    if(mid<y) ret+=query(x,y,rson,mid+1,r);
    return ret;
}
void add(int u,int v) {
    ter[++tot]=v,nxt[tot]=lnk[u],lnk[u]=tot;
}
void dfs(int u,int fa) {
    dep[u]=dep[fa]+1,f[u][0]=fa,dfn[u]=++idx,seq[idx]=u,sz[u]=1;
    for(int i=1;(1<<i)<=dep[u];++i) f[u][i]=f[f[u][i-1]][i-1];
    for(int i=lnk[u];i;i=nxt[i]) {
        int v=ter[i];
        if(v==fa) continue;
        dfs(v,u),sz[u]+=sz[v];
    }
}
int lca(int u,int v) {
    if(dep[u]>dep[v]) u^=v^=u^=v;
    for(int i=17;~i;--i) if(dep[f[v][i]]>=dep[u]) v=f[v][i];
    if(u==v) return u;
    for(int i=17;~i;--i) if(f[u][i]^f[v][i]) u=f[u][i],v=f[v][i];
    return f[u][0];
}
int getlca(int u,int v,int p) {
    int x=lca(u,v),y=lca(u,p),z=lca(v,p);
    if(dep[y]>dep[x]) x=y;
    if(dep[z]>dep[x]) x=z;
    return x;
}
int jump(int u,int d) {
    for(int i=17;~i;--i) if(d&(1<<i)) u=f[u][i];
    return u;
}
void treeModify(int u,int k) {
    int l=dfn[u],r=dfn[u]+sz[u]-1;
    if(u==root) modify(1,n,1,1,n,k);
    else if(dfn[root]<l||dfn[root]>r) modify(l,r,1,1,n,k);
    else {
        int son=jump(root,dep[root]-dep[u]-1);
        modify(1,n,1,1,n,k),modify(dfn[son],dfn[son]+sz[son]-1,1,1,n,-k);
    }
}
long long treeQuery(int u) {
    int l=dfn[u],r=dfn[u]+sz[u]-1;
    if(u==root) return query(1,n,1,1,n);
    else if(dfn[root]<l||dfn[root]>r) return query(l,r,1,1,n);
    else {
        int son=jump(root,dep[root]-dep[u]-1);
        return query(1,n,1,1,n)-query(dfn[son],dfn[son]+sz[son]-1,1,1,n);
    }
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]);
    for(int i=1;i<n;++i) {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    dfs(1,0);
    build(1,1,n);
    root=1;
    while(m--) {
        int opt;
        scanf("%d",&opt);
        if(opt==1) {
            scanf("%d",&root);
        } else if(opt==2) {
            int u,v,x;
            scanf("%d%d%d",&u,&v,&x);
            treeModify(getlca(u,v,root),x);
        } else {
            int x;
            scanf("%d",&x);
            printf("%lld\n",treeQuery(x));
        }
    }
    return 0;
}
0%