「BJOI 2006」狼抓兔子

发表于 | | 阅读次数:
字数统计: 829 字

Description

题目链接：BZOJ 1001

现在小朋友们最喜欢的”喜羊羊与灰太狼”，话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

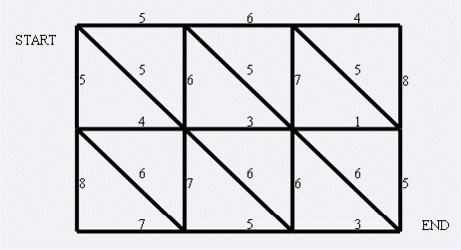
左上角点为 $(1,1)$，右下角点为 $(n,m)$（上图中 $N=3,M=4$）。有以下三种类型的道路：

  1. $(x,y)\longleftrightarrow(x+1,y)$
  2. $(x,y)\longleftrightarrow(x,y+1)$
  3. $(x,y)\longleftrightarrow(x+1,y+1)$

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的。左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角 $(1,1)$ 的窝里，现在它们要跑到右下角 $(N,M)$ 的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为 $K$，狼王需要安排同样数量的 $K$ 只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。

数据范围：$1\le N,M\le 1000$

Solution

很显然是一个裸的最小割，对 $(1,1)$ 到 $(N,M)$ 依次编号，然后按照题意建边跑最短路即可 QAQ

吐槽：终于做出了 BZOJ 的 1001（大雾

当然由于这题的图是一张平面图，所以我们也可以建出对偶图，直接跑最短路，得到的就是原图的最小割。

时间复杂度：$O((NM)^3)$（$\text{Dinic}$）

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
 
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

const int N=1e6+5,M=6e6+5;
int n,m,tot=1,lnk[N],ter[M],nxt[M],val[M],dep[N],cnr[N];

int id(int x,int y) {
    return (x-1)*m+y;
}
void add(int u,int v,int w) {
    ter[++tot]=v,nxt[tot]=lnk[u],lnk[u]=tot,val[tot]=w;
}
void addedge(int u,int v,int w) {
    add(u,v,w),add(v,u,w);
}
int bfs(int s,int t) {
    memset(dep,0,sizeof(dep));
    memcpy(cnr,lnk,sizeof(lnk));
    std::queue<int> q;
    q.push(s),dep[s]=1;
    while(!q.empty()) {
        int u=q.front(); q.pop();
        for(int i=lnk[u];i;i=nxt[i]) {
            int v=ter[i];
            if(val[i]&&!dep[v]) q.push(v),dep[v]=dep[u]+1;
        }
    }
    return dep[t];
}
int dfs(int u,int t,int flow) {
    if(u==t) return flow;
    int ans=0;
    for(int i=cnr[u];i&&ans<flow;i=nxt[i]) {
        cnr[u]=i;
        int v=ter[i];
        if(val[i]&&dep[v]==dep[u]+1) {
            int x=dfs(v,t,std::min(val[i],flow-ans));
            if(x) val[i]-=x,val[i^1]+=x,ans+=x;
        }
    }
    if(ans<flow) dep[u]=-1;
    return ans;
}
int dinic(int s,int t) {
    int ans=0;
    while(bfs(s,t)) {
        int x;
        while((x=dfs(s,t,1<<30))) ans+=x;
    }
    return ans;
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i) for(int j=1;j<m;++j) {
        int x;
        scanf("%d",&x);
        addedge(id(i,j),id(i,j+1),x);
    }
    for(int i=1;i<n;++i) for(int j=1;j<=m;++j) {
        int x;
        scanf("%d",&x);
        addedge(id(i,j),id(i+1,j),x);
    }
    for(int i=1;i<n;++i) for(int j=1;j<m;++j) {
        int x;
        scanf("%d",&x);
        addedge(id(i,j),id(i+1,j+1),x);
    }
    printf("%d\n",dinic(id(1,1),id(n,m)));
    return 0;
}
0%