「算法笔记」Link-Cut Tree

动态树问题，即要求我们维护一个由若干棵子结点无序的有根树组成的森林。要求这个数据结构支持对树的分割、合并，对某个点到它的根的路径的某些操作。

前置知识

$\text{Splay}$：博客文章详见「算法笔记」Splay 维护二叉查找树

链剖分

重链剖分

我们所谓的树剖，就是重链剖分的常用称呼。对于每个点，我们选择其最大的子树，将这条连边划分为重边，连向其余子树的边化为分轻边。

长链剖分

对每个点选择其深度最大的儿子作为重儿子，连边即为重边，其余作为轻儿子，连边即为轻边。由此得到了若干条互不相交的长链。

实链剖分

同样将某一个儿子的连边为实边，其余儿子的连边为虚边。只不过虚实是可以动态变化的，因此我们需要用更高级、更灵活的数据结构 $\text{Splay}$ 来维护每一条实链。

基于性质更加优秀的实链剖分，$\text{LCT}$（$\text{Link-Cut Tree}$）应运而生。

性质

每一个 $\text{Splay}$ 维护的是一条从上到下在原树中深度严格递增的链，且中序遍历 $\text{Splay}$ 得到的点的深度严格递增。
每个节点包含且仅包含在一个 $\text{Splay}$ 中。
边分为且仅分为实边和虚边，所有实边包含在 $\text{Splay}$ 中，而虚边总是由一棵 $\text{Splay}$ 指向另一个节点（指向该 $\text{Splay}$ 中序遍历最靠前的节点在原树中的父亲）。

为了保持树的形态，我们要让它到其他儿子的边变为虚边，由对应儿子所属的 $\text{Splay}$ 的根节点的父亲指向该点，而该点不能直接访问该儿子（认父不认子）。

操作

我们首先认识一下 $\text{LCT}$ 支持的操作类型：

查询、修改链上的信息。
对某一个树进行换根操作。
动态连边、删边。
动态维护连通性。
~~其他神奇的操作。~~

access(x)

功能：将根节点到 $x$ 上的边都变为实边。

假如我们有一棵树，实边和虚边一开始是这样划分的（图片引用于 YangZhe 的论文和 FlashHu 的博客）：

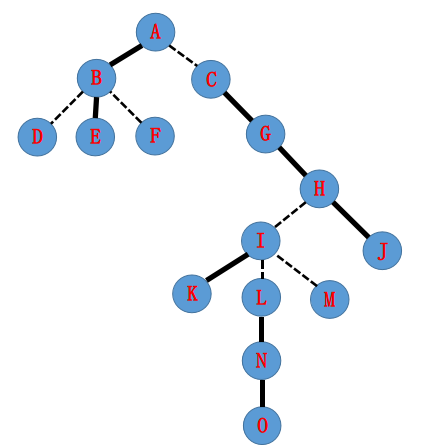
那么构成的 $\text{LCT}$ 可能长成这样（绿框中为一个 $\text{Splay}$，形态不唯一，但是只要满足中序遍历按照深度递增，对结果就没有影响）：

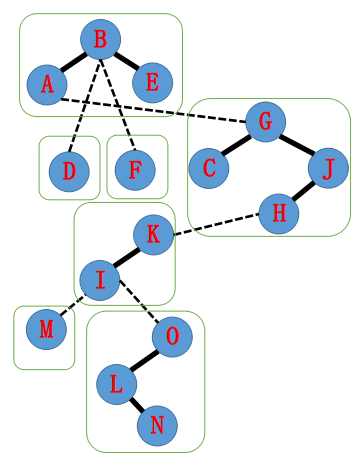
现在我们要执行 $\text{access}(N)$ 操作，把 $A\sim N$ 路径上的边都变成实边，形成一个 $\text{Splay}$。由于性质 $2$，那么肯定有些实边要变为虚边。我们可以得到这样的重新划分：

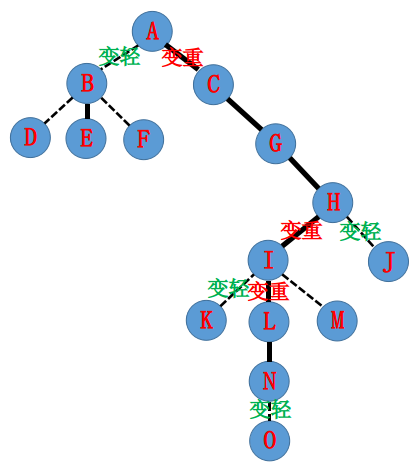
那么如何实现 $\text{access}(N)$ 的操作呢？

我们从 $N$ 这个点一步步往上进行操作。首先把 $N$ 进行 $\text{splay}$ 操作，使得它变成这个 $\text{Splay}$ 中的根节点。

为了满足性质 $2$，那么 $(N,O)$ 这条边需要从实边变为虚边。由于 $O$ 的深度比 $N$ 大，在 $\text{Splay}$ 中的表现形式就是 $O$ 在 $N$ 的右子树中，那么直接把 $N$ 的右儿子变为空（认父不认子）。得到如图形式：

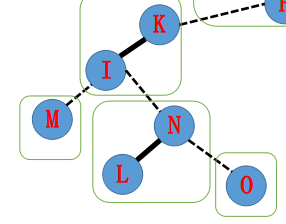
接着我们把 $N$ 所属的 $\text{Splay}$ 的虚边指向的 $I$（在原树上 $I$ 是 $L$ 的父亲）也转到所属的 $\text{Splay}$ 的根节点，那么边 $(I,K)$ 边需要变为虚边，同时去掉右儿子。这时候把 $(I,N)$ 变成实边即可。

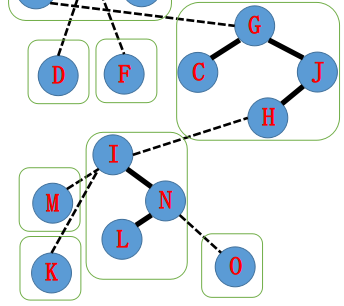
接下来同理进行一系列操作：

由于 $I$ 所属 $\text{Splay}$ 指向 $H$，故 $\text{splay(H)}$，将 $H$ 的右儿子变为 $I$。

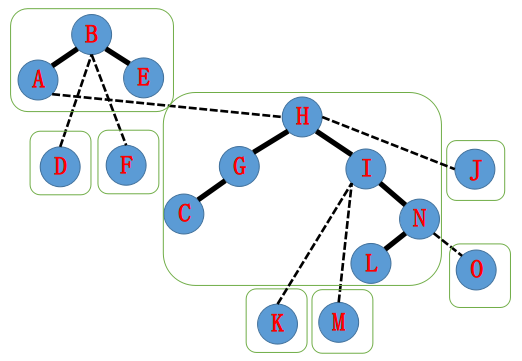
由于 $H$ 所属 $\text{Splay}$ 指向 $A$，故 $\text{splay(A)}$，将 $A$ 的右儿子变为 $H$。

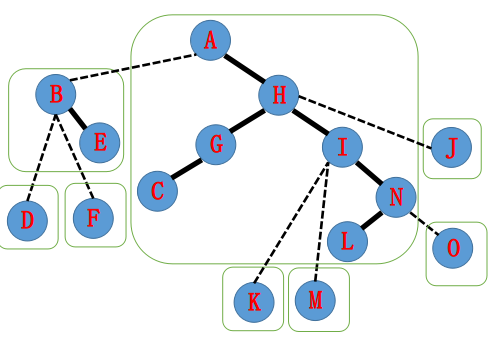
至此，$A\sim N$ 的路径上的边都变成实边了，而总结整个过程，我们发现只有如下 $4$ 步：

将节点转到所属 $\text{Splay}$ 的根。
将其右儿子删除，变为删一个 $\text{Splay}$ 的根节点。
更新节点信息。
将当前点变为虚边所指的父亲，转到步骤 $1$。

代码

1
2
3

void access(int x) {
    for(int y=0;x;x=fa[y=x]) splay(x),ch[x][1]=y,pushup(x);
}

makeroot(x)

功能：将 $x$ 成为原树的根节点。

我们首先进行 $\text{access}(x)$ 操作，这样一来我们得到了一条从根节点到 $x$ 的链，$x$ 一定是这个 $\text{Splay}$ 中深度最大的点。根据性质 $1$，在这个 $\text{Splay}$ 中 $x$ 一定没有右子树（没有比 $x$ 深度更大的点）。我们直接翻转整个 $\text{Splay}$，使得所有点的深度都倒过来，$x$ 就没有了左子树，成为了深度最小的点，也就成为了根节点。注意要给这个 $\text{Splay}$ 打上翻转懒标记。

代码

1
2
3

void makeroot(int x) {
    access(x),splay(x),rev(x);
}

findroot(x)

功能：找到 $x$ 所在的树的根，主要用来判断两点之间的连通性。

我们利用这样一个性质：一棵树的根节点一定是深度最小的点。那么我们先用 $\text{access}(x)$ 把 $x$ 先和根连成一条链，然后用 $\text{splay}(x)$ 将 $x$ 旋转到 $\text{Splay}$ 的根节点。之后根节点一定是 $x$ 不断往左走得到的（越往左深度越小）。注意在往左走的过程中一定要下传标记！

代码

int findroot(int x) {
    access(x),splay(x);
    pushdown(x);
    while(ch[x][0]) pushdown(x=ch[x][0]);
    return x;
}

split(x,y)

功能：得到 $x$ 到 $y$ 的一条路径，其中 $y$ 是为路径所在 $\text{Splay}$ 的根节点。

我们可以通过上面的函数直接写出 $\text{split}$ 函数。先把 $x$ 作为根节点，然后得到根节点到 $y$ 的链，将 $y$ 旋转到 $\text{Splay}$ 的根即可。

代码

1
2
3

void split(int x,int y) {
    makeroot(x),access(y),splay(y);
}

link(x,y)

功能：连一条虚边 $(x,y)$（如果已经连通则不操作）。

我们将 $x$ 变成原树的根，然后将 $x$ 的父节点直接设为 $y$ 即可。因为在 $\text{findroot}(y)$ 中已经执行了 $\text{access}(y)$ 和 $\text{splay}(y)$，则 $y$ 成为了所在 $\text{Splay}$ 的根节点。

连通性的检查：$x$ 成为根节点后，如果 $\text{findroot}(y)=x$ 则说明 $x,y$ 连通。

代码

void link(int x,int y) {
    makeroot(x);
    if(findroot(y)!=x) fa[x]=y;
}

cut(x,y)

功能：切断边 $(x,y)$（如果没有边则不进行操作）

首先我们把 $x$ 变成根节点，如果存在边 $(x,y)$，那么 $x$ 的深度一定比 $y$ 浅，则 $x$ 是 $y$ 的左儿子，$y$ 是 $x$ 的父节点。

但是如果不保证操作合法呢？我们需要很多条件来判断 $(x,y)$ 这条边是不存在的。不存在边 $(x,y)$ 的条件（满足一者即可）：

如果 $x,y$ 不在同一棵树内，那么不存在边。
如果 $x$ 的父亲不是 $y$，则意味着 $x,y$ 虽然在同一个 $\text{Splay}$ 中却没有连边。
如果 $x$ 的右子树非空，那么意味着以 $y$ 为根的中序遍历中 $x$ 和 $y$ 不相邻，则没有边相连。

代码

void cut(int x,int y) {
    makeroot(x);
    if(findroot(y)==x&&fa[x]==y&&!ch[x][1]) fa[x]=ch[y][0]=0,pushup(y);
}

区别

rotate(x)

功能：将 $x$ 向上旋转。

和普通 $\text{Splay}$ 不同的是，我们在修改 $x$ 的祖父的儿子时，必须判断 $x$ 的父亲是否为所在 $\text{Splay}$ 的根。因为如果不判断的话，$0$ 的儿子就会被定义为 $x$，而 $x$ 则永远不可能成为根节点，在 $\text{splay}$ 函数中将会无限循环。

代码

void rotate(int x) {
    int y=fa[x],z=fa[y],k=get(x);
    !isroot(y)&&(ch[z][get(y)]=x),fa[x]=z;
    ch[y][k]=ch[x][k^1],fa[ch[x][k^1]]=y;
    ch[x][k^1]=y,fa[y]=x;
    pushup(y),pushup(x);
}

splay(x)

功能：将 $x$ 旋转到 $\text{Splay}$ 的根节点。

由于 $\text{LCT}$ 中对 $\text{Splay}$ 有翻转操作，那么我们在 $\text{splay}(x)$ 之前，必须将 $x$ 的所有祖先的标记下放，我们用一个栈来保存所有的祖先并依次下放标记。

代码

void splay(int x) {
    int u=x,tp=0;
    st[++tp]=u;
    while(!isroot(u)) st[++tp]=u=fa[u];
    while(tp) pushdown(st[tp--]);
    while(!isroot(x)) {
        int y=fa[x];
        if(!isroot(y)) rotate(get(x)==get(y)?y:x);
        rotate(x);
    }
}

代码

以「Luogu 3690」Link Cut Tree 为例。

#include <cstdio>
#include <algorithm>
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]

const int N=3e5+5;
int n,m,fa[N],ch[N][2],val[N],sum[N],st[N];
bool r[N];

bool get(int x) {
    return rs(fa[x])==x;
}
bool isroot(int x) {
    return ls(fa[x])!=x&&rs(fa[x])!=x;
}
void rev(int x) {
    r[x]^=1,std::swap(ls(x),rs(x));
}
void pushup(int x) {
    sum[x]=sum[ls(x)]^sum[rs(x)]^val[x];
}
void pushdown(int x) {
    if(r[x]) rev(ls(x)),rev(rs(x)),r[x]=0;
}
void rotate(int x) {
    int y=fa[x],z=fa[y],k=get(x);
    !isroot(y)&&(ch[z][get(y)]=x),fa[x]=z;
    ch[y][k]=ch[x][k^1],fa[ch[x][k^1]]=y;
    ch[x][k^1]=y,fa[y]=x;
    pushup(y),pushup(x);
}
void splay(int x) {
    int u=x,tp=0;
    st[++tp]=u;
    while(!isroot(u)) st[++tp]=u=fa[u];
    while(tp) pushdown(st[tp--]);
    while(!isroot(x)) {
        int y=fa[x];
        if(!isroot(y)) rotate(get(x)==get(y)?y:x);
        rotate(x);
    }
}
void access(int x) {
    for(int y=0;x;x=fa[y=x]) splay(x),rs(x)=y,pushup(x);
}
void makeroot(int x) {
    access(x),splay(x),rev(x);
}
int findroot(int x) {
    access(x),splay(x);
    pushdown(x);
    while(ls(x)) pushdown(x=ls(x));
    return x;
}
void split(int x,int y) {
    makeroot(x),access(y),splay(y);
}
void link(int x,int y) {
    makeroot(x);
    if(findroot(y)!=x) fa[x]=y;
}
void cut(int x,int y) {
    makeroot(x);
    if(findroot(y)==x&&fa[x]==y&&!rs(x)) fa[x]=ls(y)=0,pushup(y);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i) scanf("%d",&val[i]);
    while(m--) {
        int opt,x,y;
        scanf("%d%d%d",&opt,&x,&y);
        if(opt==0) split(x,y),printf("%d\n",sum[y]);
        if(opt==1) link(x,y);
        if(opt==2) cut(x,y);
        if(opt==3) splay(x),val[x]=y;
    }
    return 0;
}

「算法笔记」Link-Cut Tree

前置知识

链剖分

重链剖分

长链剖分

实链剖分

性质

操作

access(x)

makeroot(x)

findroot(x)

split(x,y)

link(x,y)

cut(x,y)

区别

rotate(x)

splay(x)

代码

习题

维护链信息

维护连通性

维护边权

维护子树信息

维护树上染色连通块

特殊题型