$\text{Splay}$ 是一种二叉查找树,它通过不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,并且保持平衡而不至于退化为链。
结构
二叉查找树的性质
首先肯定是一棵二叉树!
能够在这棵树上查找某个值的性质:左儿子的值 $<$ 根节点的值 $<$ 右儿子的值。
节点维护信息
| $rt$ | $tot$ | $fa[i]$ | $ch[i][0/1]$ | $val[i]$ | $cnt[i]$ | $sz[i]$ |
|---|---|---|---|---|---|---|
| 根节点编号 | 节点个数 | 父亲 | 左右儿子编号 | 节点权值 | 权值出现次数 | 子树大小 |
操作
基本操作
- $\text{get}(x)$:判断节点 $x$ 是父亲节点的左儿子还是右儿子。
- $\text{pushup}(x)$:在改变节点 $x$ 的位置前,将节点 $x$ 的 $\text{size}$ 更新。
1 |
bool get(int x) { |
旋转操作
为了使 $\text{Splay}$ 保持平衡而进行旋转操作,旋转的本质是将某个节点上移一个位置。
旋转需要保证:
- 整棵 $\text{Splay}$ 的中序遍历不变(不能破坏二叉查找树的性质)。
- 受影响的节点维护的信息依然正确有效。
- $root$ 必须指向旋转后的根节点。
在 $\text{Splay}$ 中旋转分为两种:左旋和右旋。
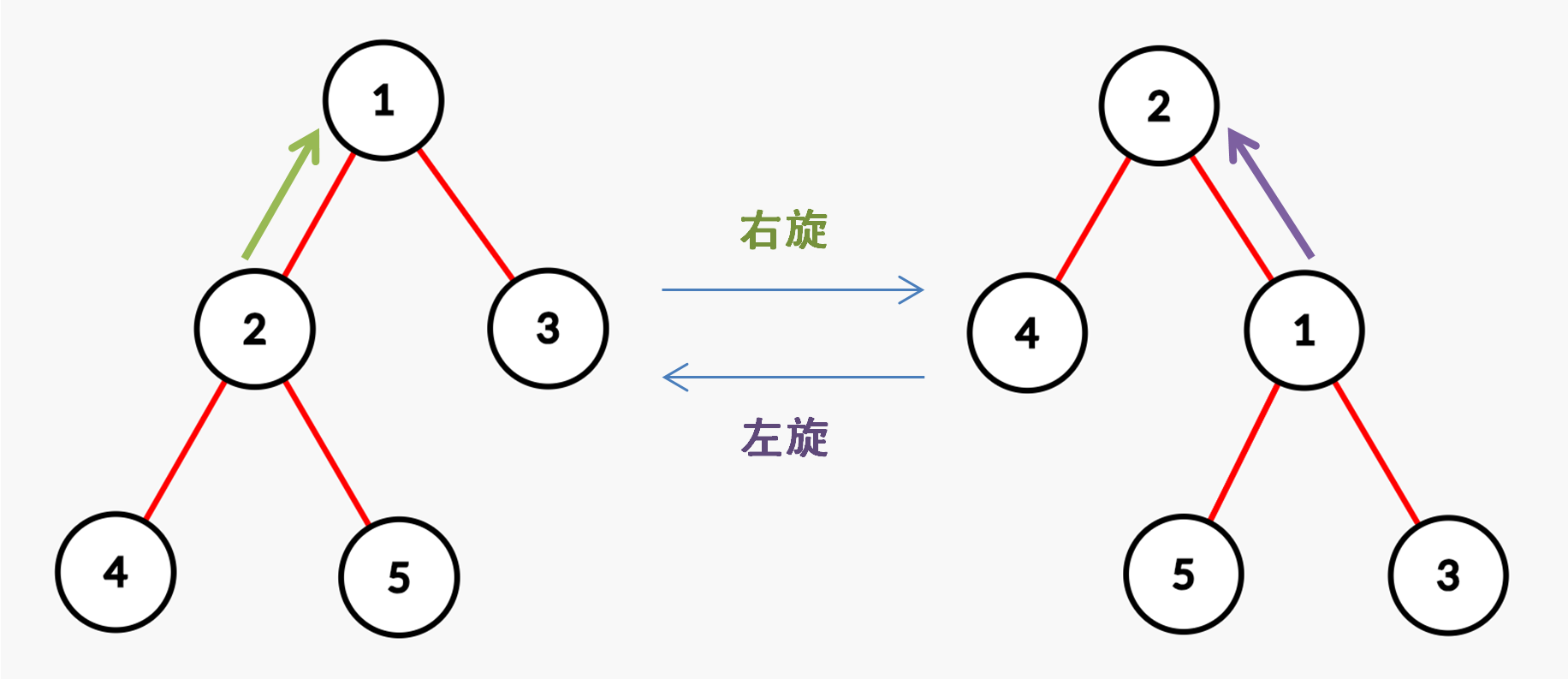
具体分析旋转步骤(假设需要旋转的节点为 $x$,$x$ 的父亲为 $y$,$y$ 的父亲为 $z$,以右旋为例)
-
将 $z$ 的某个儿子(原来 $y$ 所在的儿子位置即
get(y))指向 $x$,且 $x$ 的父亲指向 $z$。ch[z][get(y)]=x,fa[x]=z; -
将 $y$ 的左儿子指向 $x$ 的右儿子,且 $x$ 的右儿子的父亲指向 $y$。
ch[y][0]=ch[x][1],fa[ch[x][1]]=y; -
将 $x$ 的右儿子指向 $y$,且 $y$ 的父亲指向 $x$。
ch[x][1]=y,fa[y]=x; -
分别更新 $y$ 和 $x$ 节点的信息。
pushup(y),pushup(x);
1 |
void rotate(int x) { |
Splay 操作
$\text{Splay}$ 规定:每访问一个节点后都要强制将其旋转到根节点。此时旋转操作具体分为 $6$ 种情况讨论(其中 $x$ 为需要旋转到根的节点)。
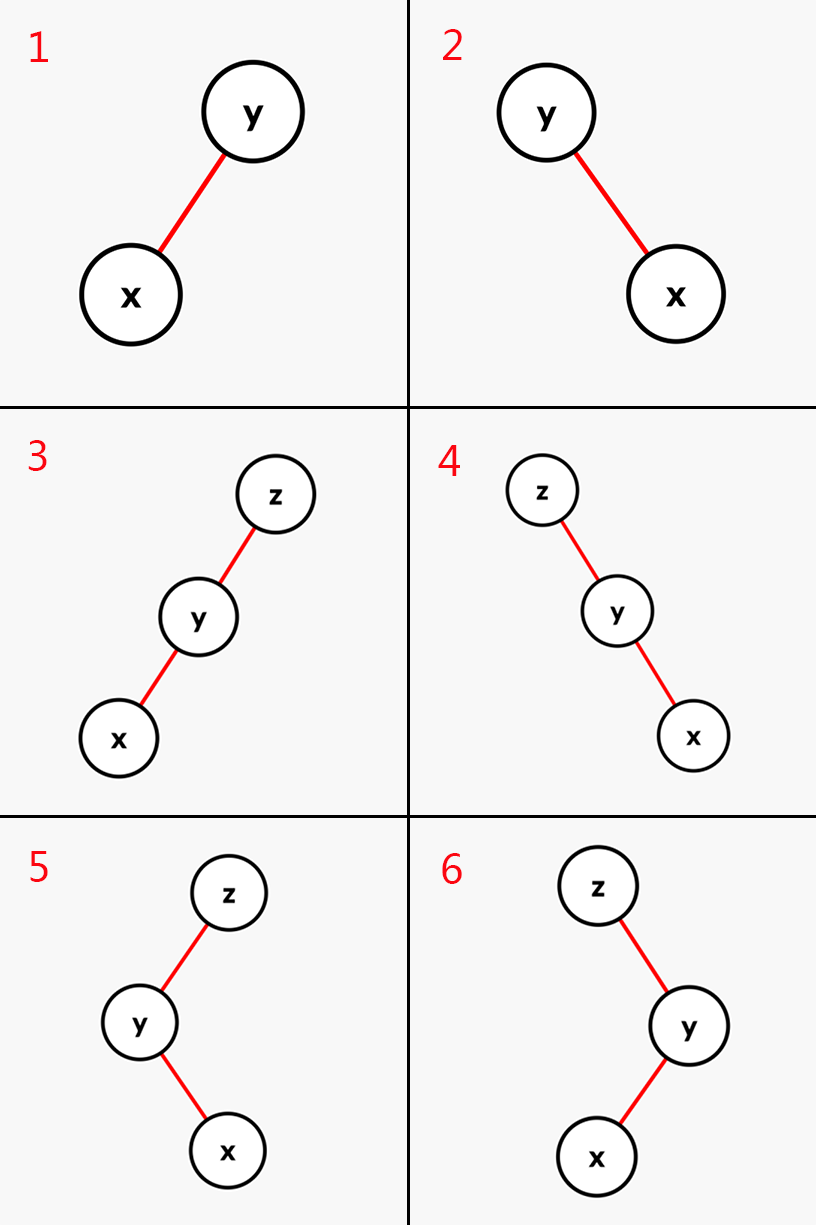
- 如果 $x$ 的父亲是根节点,直接将 $x$ 左旋或右旋(图 $1,2$)。
- 如果 $x$ 的父亲不是根节点,且 $x$ 和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 $x$ 右旋或左旋(图 $3,4$)。
- 如果 $x$ 的父亲不是根节点,且 $x$ 和父亲的儿子类型不同,将 $x$ 左旋再右旋、或者右旋再左旋(图 $5,6$)。
分析起来一大串,其实代码一小段。大家可以自己模拟一下 $6$ 种旋转情况,就能理解 $\text{Splay}$ 的基本思想了。代码 splay(x,g) 表示把 $x$ 旋转到 $g$ 的儿子(当 $g=0$ 时表示旋转到根)
1 |
void splay(int x,int g) { |
查找操作
我们有时在 $\text{Splay}$ 中查找一个值就需要查找操作。它的思想就是二叉查找树的查找过程,每次根据待查找的值 $x$ 与当前节点的值的关系,来判断进入左、右儿子。
1 |
void find(int x) { |
查询排名
排名定义为第 $1$ 个等于 $x$ 的值的排名。那么我们只需要把 $x$ 旋转到根节点,返回根的左子树的 $sz$ 再减 $1$ 即可!(代码中没有减 $1$ 的原因是笔者在 $\text{Splay}$ 中事先插入了 $-\text{INF}$ 和 $\text{INF}$)
1 |
int rnk(int x) { |
第 k 大数
设 $x$ 为剩余排名,具体步骤如下:
- 如果 $x$ 大于左子树大小与当前节点大小的和,那么向右子树查找。
- 如果 $x$ 不大于左子树的大小,那么向左子树查找。
- 否则直接返回当前节点的值。
代码中将 $x$ 增加 $1$ 的原因同上。
1 |
int kth(int x) { |
查询前驱
前驱定义为小于 $x$ 的最大的数,那么查询前驱可以转化为:将 $x$ 旋转到根节点, 前驱即为 $x$ 的左子树中最右边的节点。注意当 $x$ 不存在时,根节点的值比 $x$ 小的情况要特判!
1 |
int pre(int x) { |
查询后继
后继定义为大于 $x$ 的最小的数,查询方法和前驱类似:$x$ 的右子树中最左边的节点。
1 |
int suc(int x) { |
插入操作
插入操作是一个非常重要的操作:按照二叉查找树的性质向下查找,找到待插入的值 $x$ 应该插入的节点并插入。如果 $x$ 原来就存在,那么直接更新 $cnt$,否则新建一个空节点。最后别忘了 $\text{Splay}$ 操作。
1 |
void ins(int x) { |
删除操作
删除操作看似是一个比较复杂的操作,但是如果深入理解了 $\text{Splay}$ 的性质,其实非常简单!
- 首先得到 $x$ 的前驱 $lst$ 和后继 $nxt$。将 $lst$ 旋转到根,将 $nxt$ 旋转到 $lst$ 的儿子(显然是右儿子)。
- 观察这个过程可以发现:如果 $x$ 存在,那么此时 $nxt$ 的左儿子一定就是 $x$,将这个节点的大小减 $1$ (需要 $\text{splay}$ 操作)或者直接删除即可。
1 |
void del(int x) { |
代码
1 |
|